Understanding how things change is a key part of math and science — and that’s exactly what derivatives help us do. Whether you’re a student, a researcher, or just curious about calculus, this article will help you understand what derivatives are, why they matter, and how to use them.

In this article, we’ll explore what derivatives are, their importance, and the key rules used to calculate them.

📘 What is a Derivative?

In simple terms, a derivative measures how a function changes as its input changes. It tells you the rate of change or the slope of a function at any given point.

This formula is called the limit definition of a derivative.

🎯 Where Are Derivatives Used?

Derivatives have countless applications across disciplines:

• Physics: To find velocity, acceleration, and rates of motion.

• Economics: To calculate marginal cost, marginal revenue, or profit.

• Biology: To model population growth or drug absorption rates.

• Engineering: For designing stable structures and systems.

• Machine Learning: Used in optimization methods like gradient descent.

  ✨ Real-Life Examples of Derivatives

  Derivatives may sound abstract, but they’re used all the time in real-world scenarios:

  🚗 Physics:

  • Speed is the derivative of position with respect to time.

  • Acceleration is the derivative of speed with respect to time.

  💹 Economics:

  • Marginal cost: How much does cost increase when producing one more unit?

  • Marginal revenue: The additional income from selling one more product.

  🌿 Biology:

  • Modeling population growth or bacteria spread.

  🤖 Artificial Intelligence:

  • Derivatives are used in gradient descent algorithms to optimize models.

• 📏 Basic Rules of Derivatives

  To make differentiation easier, mathematicians have developed several rules. Let’s break down the most commonly used ones:

  1. Power Rule

  

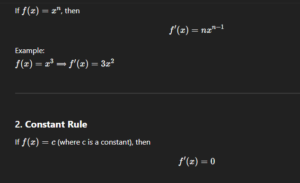
• 🔍 Why are Derivatives Important?

  • Engineering: Analyze changing forces and structures.

  • Economics: Understand growth trends and optimize functions.

  • Medicine: Model disease spread and drug absorption rates.

  • Machine Learning: Used in optimization algorithms like gradient descent.

  • 🧠 Final Thoughts

    Understanding derivatives is crucial for solving real-world problems involving rates of change. Whether you’re a student or a professional, mastering the basic rules of derivatives can help you tackle challenges in science, business, and technology.

  • 
  • Trends in Apple Production in Pakistan: A Historical Overview (1957–2023)

• For more details click here