Introduction

Multicollinearity refers to a situation in multiple regression models where two or more independent variables are highly correlated with each other. This high correlation can make it difficult to isolate the individual effect of each independent variable on the dependent variable. In other words, multicollinearity occurs when the independent variables in the regression model provide redundant information.

Impact of Multicollinearity on the Estimation of Regression Coefficients:

1. Inflated Standard Errors:

   • When multicollinearity is present, the standard errors of the regression coefficients tend to become larger. This makes the estimates less precise.

   • Larger standard errors can lead to insignificant t-statistics, meaning that it becomes harder to determine if a variable has a statistically significant relationship with the dependent variable.

2. Unstable Coefficients:

   • In the presence of multicollinearity, the coefficients of the correlated variables may become highly sensitive to small changes in the data. This leads to unstable or erratic coefficient estimates, meaning that small variations in the sample data may cause large fluctuations in the estimated coefficients.

3. Incorrect Inference:

   • Multicollinearity makes it difficult to assess the individual contribution of each predictor variable. Therefore, making inferences about the effect of each variable on the dependent variable becomes unreliable.

   • As a result, you may misinterpret the importance or influence of predictors in the model.

4. Overfitting:

   • High multicollinearity can result in an overfitted model, where the model fits the training data very well but performs poorly on new data (lack of generalization).

---

Methods to Detect Multicollinearity:

Variance Inflation Factor (VIF):

• VIF measures how much the variance of an estimated regression coefficient increases when your predictors are correlated. A high VIF indicates high multicollinearity.

• A VIF value greater than 10 is often considered indicative of significant multicollinearity.

Formula for VIF: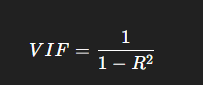

1. Correlation Matrix:

   • You can check the correlation matrix between independent variables. High correlation (usually above 0.7 or 0.8) between two or more independent variables suggests multicollinearity.

2. Condition Index:

   • A condition index greater than 30 indicates possible multicollinearity. This index is derived from the eigenvalues of the scaled and centered design matrix.

3. Tolerance:

   • The tolerance value is the reciprocal of VIF. A tolerance value lower than 0.1 indicates multicollinearity.

---

Methods to Address Multicollinearity:

1. Remove One of the Correlated Variables:

   • If two variables are highly correlated, you can remove one of them from the model. This reduces redundancy and eliminates multicollinearity.

2. Combine the Correlated Variables:

   • If the variables are measuring the same underlying concept, consider combining them into a single composite variable through techniques such as Principal Component Analysis (PCA) or Factor Analysis.

3. Increase Sample Size:

   • Increasing the sample size can sometimes help reduce the effects of multicollinearity by providing more data for the model to discern the true relationships between variables.

4. Use Regularization Techniques:

   • Techniques like Ridge Regression and Lasso Regression add penalties to the regression model to shrink the coefficients of less important variables, helping to deal with multicollinearity. These techniques are especially useful in cases where the independent variables are highly correlated.

5. Center the Variables:

   • Mean centering (subtracting the mean of each predictor variable) can sometimes help reduce multicollinearity, especially when dealing with interaction terms or polynomial regression.

6. Principal Component Regression (PCR):

   • In PCR, the original predictors are transformed into a set of orthogonal components (principal components). These components are then used in the regression model, which helps mitigate the problem of multicollinearity.

---

Conclusion:

Multicollinearity can distort the regression analysis by inflating standard errors and making the coefficients unstable. It is essential to detect and address multicollinearity to ensure accurate and reliable regression models. Methods such as checking VIF, removing correlated variables, and using regularization techniques can help overcome this issue.

internal link 

For more information